3 Economic Modelling and Scope of Analysis
Economic modelling at PHARMAC has two distinct phases.
Phase 1
Obtain clinical evidence
(Chapter 4)
Phase 2
Process evidence to estimate effectiveness and relative cost-effectiveness of the pharmaceutical for the proposed indication(s) in the New Zealand clinical setting
Decisions have to be made regardless of data availability. Modelling in economic analysis extrapolates from available data to best inform decision making at a particular point in time (7).
Health economic models combine information about disease progression, the relative clinical effectiveness of a pharmaceutical, and the costs and savings associated with the funding of a pharmaceutical, all obtained from the best available evidence. The overall structure of an economic model is outlined in the diagram below:
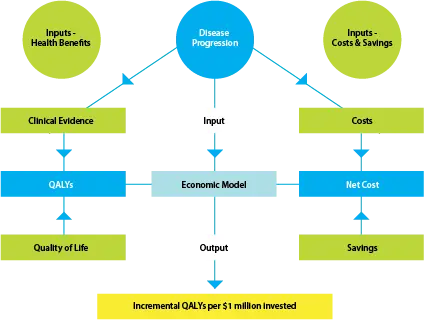
3.1 Models
Key Recommendation: Models should avoid unnecessary complexity and should be transparent, well described and reproducible.
Models consist of a series of branches, representing the expected health outcomes of different treatments. It is important these models capture all the appropriate additional benefits and costs.
3.1.1 Model Transparency
Model inputs and assumptions need to be clearly stated and the rationale for the inputs and assumptions documented and explained. Models should be transparent and the structure, data and process of building the model should be detailed enough to enable competent analysts who are not familiar with the model to confirm that it functions correctly and to reproduce it. Unnecessary complexity in economic models should be avoided.
3.1.2 Scope of Model
The simplest model type should be chosen, providing it captures the essential features of the disease and interventions, and all relevant data are incorporated.
The models PHARMAC prefers are either simple decision trees or Markov models (8-12)
Simple Decision Trees
Simple decision trees can be used in cases where an event may happen only once, during a discrete period, and the patients are not at continuous risk of recurrence. For example, a simple decision tree could be used to model an acute episode of illness leading to either full recovery or death.
Markov Models
Markov models assume that a person is always in one of a finite number of health states. The model is usually started with a cohort assigned to an initial health state (or Markov state). People then move between states at defined recurring intervals (Markov cycles), as determined by the transition probabilities.
A branch of a Markov model is shown below. In this example, all patients begin in the ‘Alive’ health state, and are then at risk of having an adverse event, which they may recover or die from. The model would also incorporate the disease-specific mortality rate of the target population. The model is usually run for enough cycles that all of the cohort moves through to the ‘Dead’ state: in other words, a lifetime horizon.
Figure 1: Typical Markov Model structure
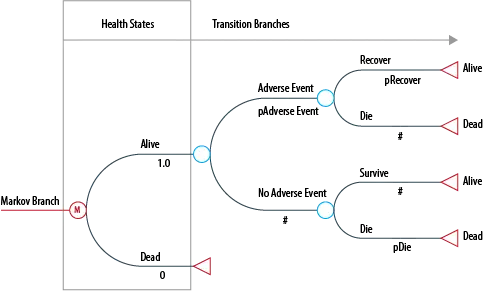
Each of the Markov states is assigned a utility based on a health-related quality of life weight. The total quality-adjusted life years (QALYs) measured in each arm is the utility for each state multiplied by the time in years spent in each state.
Markov models are useful when the time horizon spans more than a few discrete time periods, when events can recur, or when the timing of events is uncertain.
3.1.3 Health States
Health states included in a model should correspond to the underlying disease progression and/or health status.
3.2 Time Horizon and Cycle Length
Key Recommendation: In the majority of CUAs, a lifetime horizon should be used and half-cycle adjustment applied.
The time horizon should extend far enough into the future to capture all the major clinical and economic outcomes of the alternatives under assessment.
In general, a lifetime horizon should be used to estimate differences in expected survival duration. However, for conditions that are unlikely to exist over a lifetime, or where there is uncertainty around whether survival benefits will persist, the choice of a shorter time horizon (eg until recovery or death) can be justified, providing there are no differences in mortality, long-term morbidity and cost between the alternative options. The report should always justify the time horizon used in the analysis.
3.2.1 Cycle Length
The cycle length should be the minimum time period over which pathology and/or symptoms in patients are expected to alter, and should be based on the nature of the disease rather than the availability of data (10). For example, if clinical events are likely to occur frequently, a short cycle length should be used. The chosen cycle length should not have an impact on the results of the analysis.
3.2.2 Half-Cycle Correction
Markov models assume that a patient’s time in a state is constant for the duration of the cycle, and that transitions between states occur at discrete points of time at the beginning or end of the cycle. However, transition probabilities that are derived from a continuous rate, such as mortality, effectively assume that transitions occur on average halfway through the cycle. These unaligned transitions and mean probabilities may result in over- or under-estimating health outcomes. Therefore an unbiased estimate should ensure that, on average, patients move between states halfway through the cycle. A half-cycle correction can achieve this adjustment (10, 11).
If a half-cycle correction is not applied, an explanation needs to be provided for why the model does not require it.
3.3 Perspective and Decision Problem
Key Recommendation: Undertake analyses from the perspective of the funder, with regard to PHARMAC’s Factors for Consideration. Always clearly state the decision problem.
3.3.1 Perspective
PHARMAC base-case cost-utility analyses are undertaken from the perspective of the funder. The key reason is that PHARMAC’s statutory objective requires it to achieve “the best health outcomes” “for eligible people”, and to do so “within the funding provided”.
PHARMAC’s Factors for Consideration are a framework for ensuring that relevant benefits, costs, savings, and other aspects are taken into account. The economic assessments described in this Prescription for Pharmacoeconomic Analysis can help to inform consideration of many, but not all of the Factors.
3.3.2 Decision Problem
All analyses should include a clear statement about the decision problem that prompted the analysis. This should include information about the disease, patient population, and treatment options available [2].
3.4 Target Population
Key Recommendation: The target population is the New Zealand population most likely to receive treatment. It may be necessary to use subgroup analyses if treatment can be targeted to those most likely to benefit. However, subgroup analyses should not be used when there is no overall treatment effect in the intention-to-treat population or primary endpoint. In cases where the subgroup was defined retrospectively in the clinical trial(s), the data should be used cautiously and evidence of statistical heterogeneity reported.
The target population is the New Zealand population most likely to receive treatment. Any differences between the population in the key clinical trials and the target population should be discussed in the report.
Analyses for population subgroups should be used if value for money can be improved by targeting funding to those who are most likely to benefit, for example through the use of Special Authority criteria. Please refer to Chapter 4 for subgroup analysis methods.
3.5 Comparator(s)
Key Recommendation: The comparator(s) used in analyses should be the funded treatment (available on the Pharmaceutical Schedule or by DHB hospitals) that most prescribers or clinicians would replace in New Zealand clinical practice, and the treatment prescribed to the largest number of patients (if this differs from the treatment most prescribers would replace).
The comparator(s) used in PHARMAC analyses should be funded in New Zealand and be:
- the funded treatment that most prescribers or clinicians would replace in New Zealand clinical practice; and/or
- the treatment given to the largest number of patients, if this differs from the treatment most prescribers or clinicians would replace.
The analysis should consider both current clinical practice and likely future practice (ie the treatment regimen at the time the pharmaceutical is likely to be funded). This allows for any changes that may occur in treatment regimens over time.
The comparator used in the model should not be constrained by data availability. It is acceptable and often appropriate to use a comparator even if there are no direct studies between that comparator and the proposed intervention. Further details on making such comparisons are given in the modelling section.
In cases where treatment regimens differ substantially throughout New Zealand, it is recommended that a range of comparators be used in the analysis. The results of the analysis using the different comparators should be reported separately, as well as reporting a weighted average of the QALYs per $1 million invested result. The result should be weighted by the estimated patient numbers prescribed the comparator treatments, as described in section Weighting of results from multiple models 9.2.
If there is any uncertainty about the most appropriate comparator to use in the CUA, it is recommended that expert clinical advice be sought. The Pharmacology and Therapeutic Advisory Committee (PTAC) often performs this role for analyses conducted by PHARMAC.


